Pier Maria Boria

VERSIONE STAMPABILE (REV.10 2010) PARTE PRIMA

S'INVITA A LEGGERE LA VERSIONE STAMPABILE

English version refreshed in 2013

ENGL. VERSION clicking here OF THE PAGES 1-5
PG. 6-10
PG. 11-15
PG. 16-20
PG. 21-25
PG. 26-31

VERSIONE STAMPABILE (REV. 10 2009) PARTE SECONDA


              THERMODYNAMIC & LIFE
                (TTC - Thermodynamic theory of Creation)                                                                                                       TERMODINAMICA & VITA
(TTC - Teoria termodinamica della Creazione)

Thermodynamic Theory of Creation (TTC)

ABSTRACT

In this age of quick communications, one of the most abused adjectives is the term “scientific” and the origin of this abuse can be found in the  misinterpretation of the true scientific method.
As a matter of fact, the proper realization of any construction, both mechanic and intellectual, needs of an adequate basis: concerning this TTC, the basis and the bearing pillars are made of Classical Physics arguments, full blown and accepted by the universal scientific community.

They are:
• The second Principle of Thermodynamic in Clausius’ version, introducing the entropic properties of transformation;
• The distribution probability of identical objects on different levels following Boltzmann’s Statistics;
• The case, contemplated by Gauss’ Law.

As an example associated with probability and case, the Eddington’s paradox has been chosen. It deals with monkeys who have the ability to type and have developed a numerical aspect leading to the conclusion that the probability of obtaining predefined complex systems (a book of only about a thousand of pages) by positioning given objects on different level is practically nothing.
With these reasonable work hypotheses, when accidental events are overlapped by probable ones, sustaining the self-organization of the matter becomes a “mission impossible”.

Coordinating the reasoning developed, the TTC states that:

1. While the observable transformations in the mineral field proceed following an increase in Entropy, only living systems are characterized by the continuous production (and not cyclical) of “negative” Entropy (as Prigogine would say, mentor of the New Physics).
2. The organized complexity cannot be born “sua ponte” (by itself) with probability statistical considerations.
3. The case, considered on its popular meaning, doesn’t exist. If it existed, Gauss couldn’t have written the “Law of Case”.
4. In a scientific discussion, who speaks about case as of a Deus ex machina, able to solve difficult situations, doesn’t belong to a healthy scientific doctrine (the term “case” is used with an excessive and senseless nonchalance!).
5. Believing that sink systems, subjects of irreversible transformations (the only ones which can be realized in Experimental Physics), are able to produce negative Entropy, from a scientific point of view it means to believe in the possibility of perpetual motion.

For these reasons, the final statement of TTC is: “Creation is a thermodynamic need”.

In the essay “Thermodynamic & Life” the three fundamental pillars used (Entropy, Statistics, Randomness) and the entire work are supplied with information to dispense the consultation of more or less scattered bibliographical material. As a matter of fact, the purpose was to produce a complete work of all those Classical Physics ideas necessary and sufficient to make it comprehensible to everybody.

Suggested improvements are appreciated.

PMB

Teoria termodinamica della Creazione (TTC) 



RIASSUNTO

Uno degli aggettivi più abusati, in questa era di rapide comunicazioni, è “scientifico” e l’origine dell’abuso va ricercata nella misconoscenza del vero metodo scientifico.
Infatti la corretta realizzazione di una qualunque costruzione, sia essa meccanica che intellettuale, necessita di adeguate fondamenta: nel caso di questa TTC le fondamenta ed i pilastri portanti sono costituiti da argomenti di Fisica Classica conclamati ed accettati dalla comunità scientifica universale.

Essi sono:
• Il secondo Principio della Termodinamica nella versione di Clausius che introduce le proprietà entropiche delle trasformazioni;
• la probabilità della distribuzione di oggetti identici su più livelli secondo la Statistica di Boltzmann
• il caso, contemplato dalla Legge di Gauss.

Come evento esemplificativo, associato alla probabilità ed al caso, è stato scelto il Paradosso di Eddington riguardante le scimmie dattilografe: se ne è sviluppato l’aspetto numerico, giungendo alla conclusione che la probabilità di ottenere sistemi complessi predefiniti (un libro di solo un migliaio di pagine) dal posizionamento di dati oggetti su dati livelli è praticamente nulla.
Quando, poi, con ipotesi di lavoro ragionevoli, si sovrappongono gli effetti casuali a quelli probabili, il sostenere l’auto-organizzazione della materia diventa una “mission impossible”

Coordinando i ragionamenti via via sviluppati, la TTC sostiene che:

1. Mentre le trasformazioni osservabili nel regno minerale procedono nel senso cui compete un incremento di Entropia, solo i sistemi viventi sono caratterizzati dalla produzione continua (e non ciclica) di Entropia “negativa” (come direbbe Prigogine, mentore della Nuova Fisica).
2. La complessità organizzata non può nascere “sua sponte” con considerazioni statistiche di probabilità.
3. Il caso, nel senso inteso dall’accezione popolare, non esiste. Se esistesse, Gauss non avrebbe potuto scrivere la “Legge del caso”.
4. Chi parla di caso, in una disquisizione scientifica, come di un Deus ex machina, in grado di risolvere situazioni scabrose, è fuori da una sana dottrina scientifica (il termine caso è usato con eccessiva ed insensata disinvoltura!).
5. Credere che i sistemi dissipativi, soggetti di trasformazioni irreversibili (le uniche realizzabili in Fisica Sperimentale), siano in grado di produrre Entropia negativa, dal punto di vista scientifico è equivalente a credere nella possibilità del moto perpetuo.

Cosicché l’asserto conclusivo della TTC afferma: “la Creazione è una necessità termodinamica”.

Nel saggio “Termodinamica & Vita” i tre pilastri fondamentali utilizzati (Entropia, Statistica, Casualità) e l’intera trattazione, sono corredati delle informazioni atte a dispensare la consultazione di materiale bibliografico più o meno sparso. Si è cercato, infatti, di produrre un lavoro completo dei richiami di Fisica Classica necessari e sufficienti per renderlo comprensibile a tutti.

Sono graditi suggerimenti migliorativi.

PMB

PARTE 1 (di 2)

1. L’ENTROPIA

Per comprendere il significato dell’Entropia, primo pilastro di questo nostro saggio, ci sembra utile iniziare dalla sua definizione qualitativa più generalizzata: è un indice dello stato di disordine di un determinato insieme di corpi. Maggiore è il disordine, maggiore è l’Entropia (“Entropia, sinonimo di disordine”: Helmholtz, 1821-1894).
Procederemo a ritroso fino alla sua prima enunciazione, di origine strettamente termodinamica.
Per fissare le idee, consideriamo il seguente insieme: una stanza con all’interno di essa un tavolo con sopra una bottiglia, chiusa, piena di fumo (alla “soliti ignoti” a San Vittore...). Un osservatore fotografa a testimonianza dello stato di ordine iniziale: si distingue la bottiglia, il tavolo, il fumo, che è raccolto in un ben identificato volume, oltre alla stanza (che costituiscono il nostro ”universo”: sistema in osservazione + ambiente).
Aprendo la bottiglia, Figura 1, si otterrà la diffusione del fumo nella stanza: dopo un certo tempo (diciamo un giorno) l’osservatore potrà fotografare uno stato di maggior disordine: il fumo è uscito dalla bottiglia.



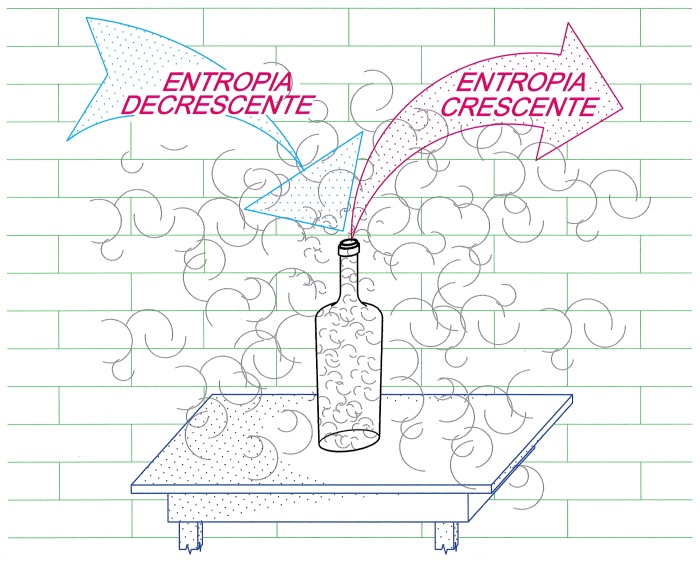
Figura 1 – La trasformazione ad entropia crescente è la più probabile, mentre la probabilità che si verifichi spontaneamente quella ad entropia decrescente è “praticamente nulla”


Si può pensare che, dopo un milione di giorni, il tavolo sia finito in polvere o che, comunque, le interazioni di questo universo con altri (a causa, ad esempio, di un cataclisma) abbia prodotto la distruzione anche del tavolo e della bottiglia e poi della stessa stanza: l’osservatore scatterà un’altra fotografia.
Poiché le osservazioni possono essere pensate prolungarsi per un tempo illimitato, le fotografie, in successione, indicheranno uno stato di disordine, di caos, ovvero di Entropia, crescente.
A questo punto dovrebbe essere chiaro che, quanto più ordinato è il risultato finale della trasformazione pensata, minore è la probabilità che si realizzi; ed in pratica si può dire che una probabilità estremamente bassa equivalga all’impossibilità.
Adottando il linguaggio di Prygogine: le trasformazioni verso entropia crescente “producono” entropia positiva (la differenza di entropia tra lo stato finale e quello iniziale ≥ 0), mentre quelle ad entropia decrescente producono entropia negativa.
Procedendo storicamente a ritroso osserviamo che il concetto di entropia fa il suo ingresso in Fisica grazie ai lavori di Clausius (Germania, 1822-1888), che era alla ricerca dei principi di conservazione che governano la Termodinamica.

I principi di conservazione (che risopondono alla domanda "cosa rimane invariato dopo una trasformazione?") rappresentano i pilastri di qualunque disciplina scientifica.

Curiosamente egli s’imbatté in un principio di non conservazione!, e giunse a definire un indice di stato che qualcuno definisce anomalo e che egli chiamò Entropia.
Quindi, inizialmente, il concetto di Entropia era strettamente termodinamico (gli stati dei sistemi in osservazione dipendevano da variabili come temperatura, pressione e volume), mentre le osservazioni con cui abbiamo iniziato, come detto, sono generalizzazioni qualitative macroscopiche.
Ricordiamo, ad esempio, tra gli altri, il Principio di Conservazione dell’Energia ed il Principio di Conservazione del Momento della Quantità di Moto (o Momento Angolare, ingl.: Angular Momentum).
L’Entropia risulta un ente non conservativo (salvo nelle trasformazioni reversibili, del tutto teoriche): nelle trasformazioni realizzabili nella pratica, in cui si ha un’interazione tra sistema in osservazione e l’ambiente, il soggetto in esame risulta più ricco di Entropia dopo la trasformazione (questo consente di prevedere in che direzione andrà la trasformazione).
In Figura 2 un esempio: un corpo “freddo” a temperatura T₁ viene messo in contatto con un corpo “caldo” a temperatura T₂: le variabili sono la quantità di calore scambiata Q e le temperature; l’esperienza ci dice che la quantità di calore Q passerà dal corpo a temperatura maggiore a quello a temperatura minore (postulato di Clausius) fino al raggiungimento di una temperatura di equilibrio T_e intermedia tra le due.




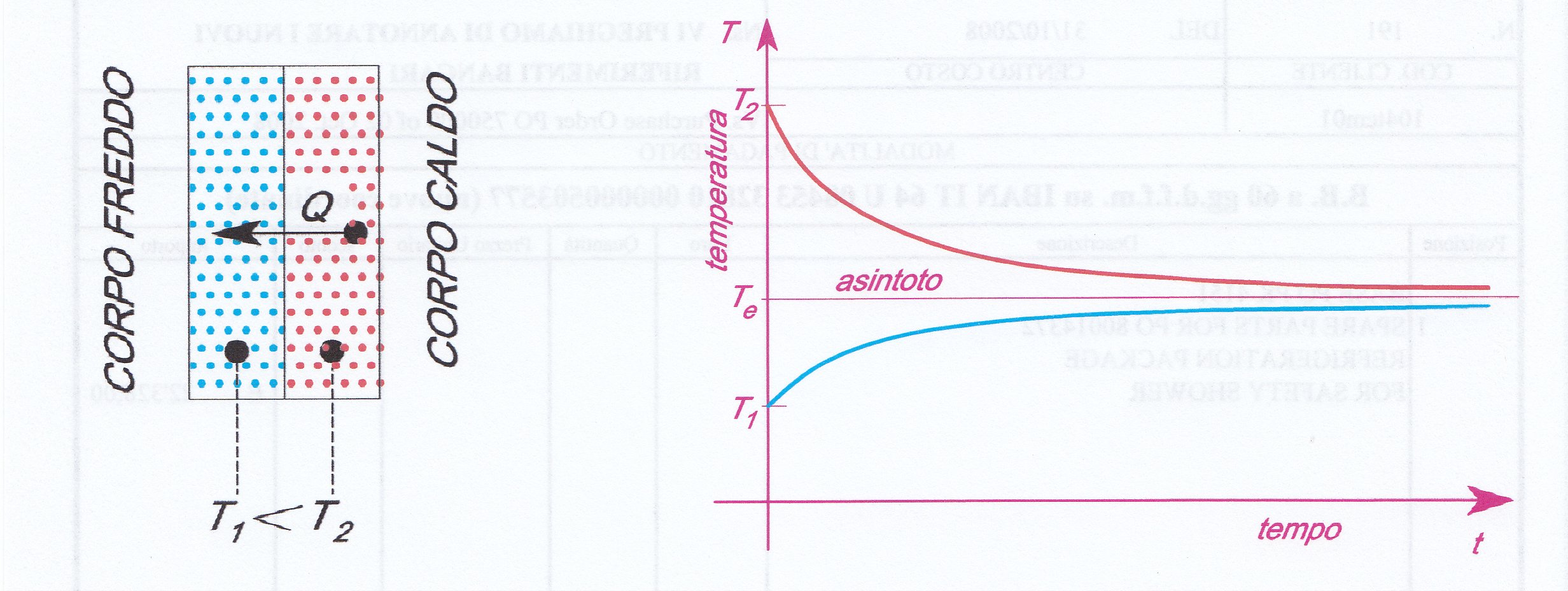
Figura 2 – Per il Postulato di Clausius

Clausius osserva che la relazione tra la quantità di calore “trasformata”, Q, e le temperature, finale ed iniziale, è

 

dal momento che



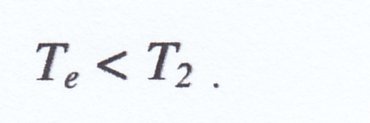
Clausius chiamò Entropia il rapporto S = Q/T.
Utilizzando le notazioni correnti possiamo dire che il calore scambiato ha realizzato una trasformazione in cui




2. ANALOGIA TRA ENTROPIA E PESO

Il contenuto di questo paragrafo è inessenziale ai fini del presente saggio; tuttavia ci sembra utile per completare quanto si dice sull’Entropia.
Tra i fisici del XIX secolo, cultori di Termodinamica, Zeuner (Germania 1828-1907) propose un’ interessante analogia tra l’energia potenziale gravitazionale di un peso P e l’Entropia di una massa avente un calore Q ad una temperatura T.
Con riferimento alla Figura 3 sappiamo che l’energia potenziale (cioè il lavoro meccanico che può compiere) della massa d’acqua del bacino è L = P · ΔH.





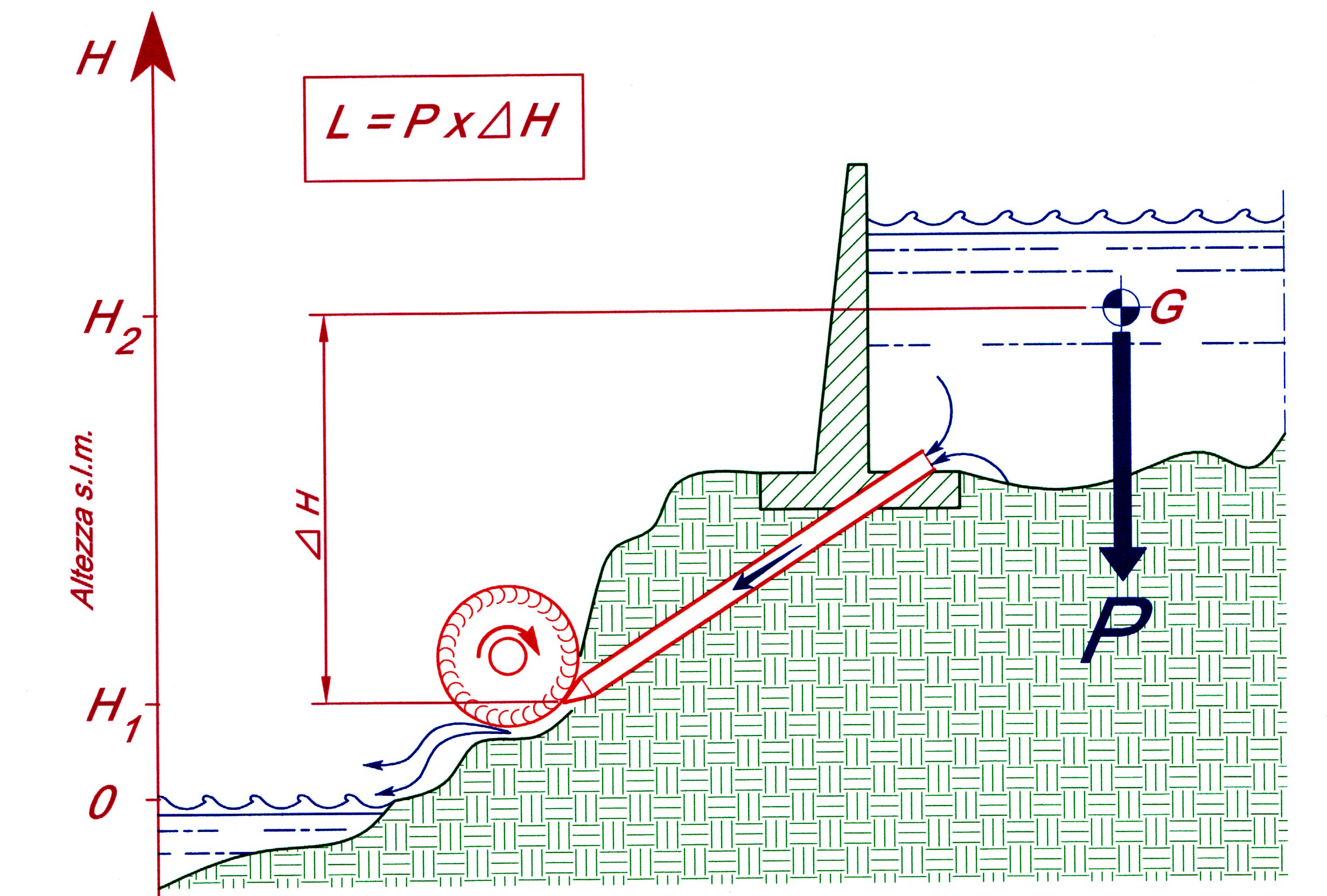
Figura 3 – Sistema per trasformare l’energia potenziale gravitazionale in energia meccanica ad un albero motore


Zeuner considera il lavoro ottenibile da un motore termico in grado di trasformare il calore in lavoro con un Ciclo di Carnot (un motore a benzina realizza un Ciclo Otto, uno a gasolio realizza un Ciclo Diesel, un motore esotermico a vapore realizza un Ciclo Rankine etc.), dal momento che consente di esprimere il rendimento di trasformazione calore/lavoro in termini di sole temperature (anziché di quantità di calore) e ci conduce allo scopo.
Infatti, com’è arcinoto, si dimostra che il rendimento del Ciclo Carnot è



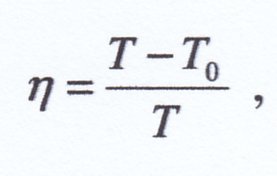
laonde per cui, introducendo nel motore la quantità di calore Q, il lavoro meccanico L ottenibile sarà:



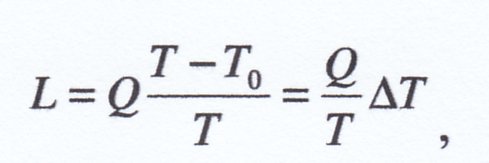
ovvero l’espressione che compare nella Figura 4, dove l’entropia Q/T ha una funzione analoga al peso P ed il salto di livello ΔH corrisponde al salto di temperatura ΔT che il motore riesce a realizzare (essendo Δ’T < Δ”T si ha, in proporzione, L’ < L”, ovviamente le energie interne residue, allo scarico, non trasformate in lavoro, saranno U’ > U”).
Osserviamo che tra Q e T esiste un legame funzionale tale per cui incrementando Q incrementa in proporzione diretta T (essendo lecito ritenere costante il calore specifico della massa che percorre il ciclo) e, quindi, data una certa entropia iniziale, il lavoro ottenibile dipende esclusivamente dal ΔT realizzabile.
Il motore che espelle allo scarico calore a minor temperatura produce più lavoro meccanico a parità di “consumo”: questo è il significato del raffronto tra i due motori termici, funzionanti con “salti” di temperatura diversi, e medesima Entropia iniziale, considerati nella Figura 4.




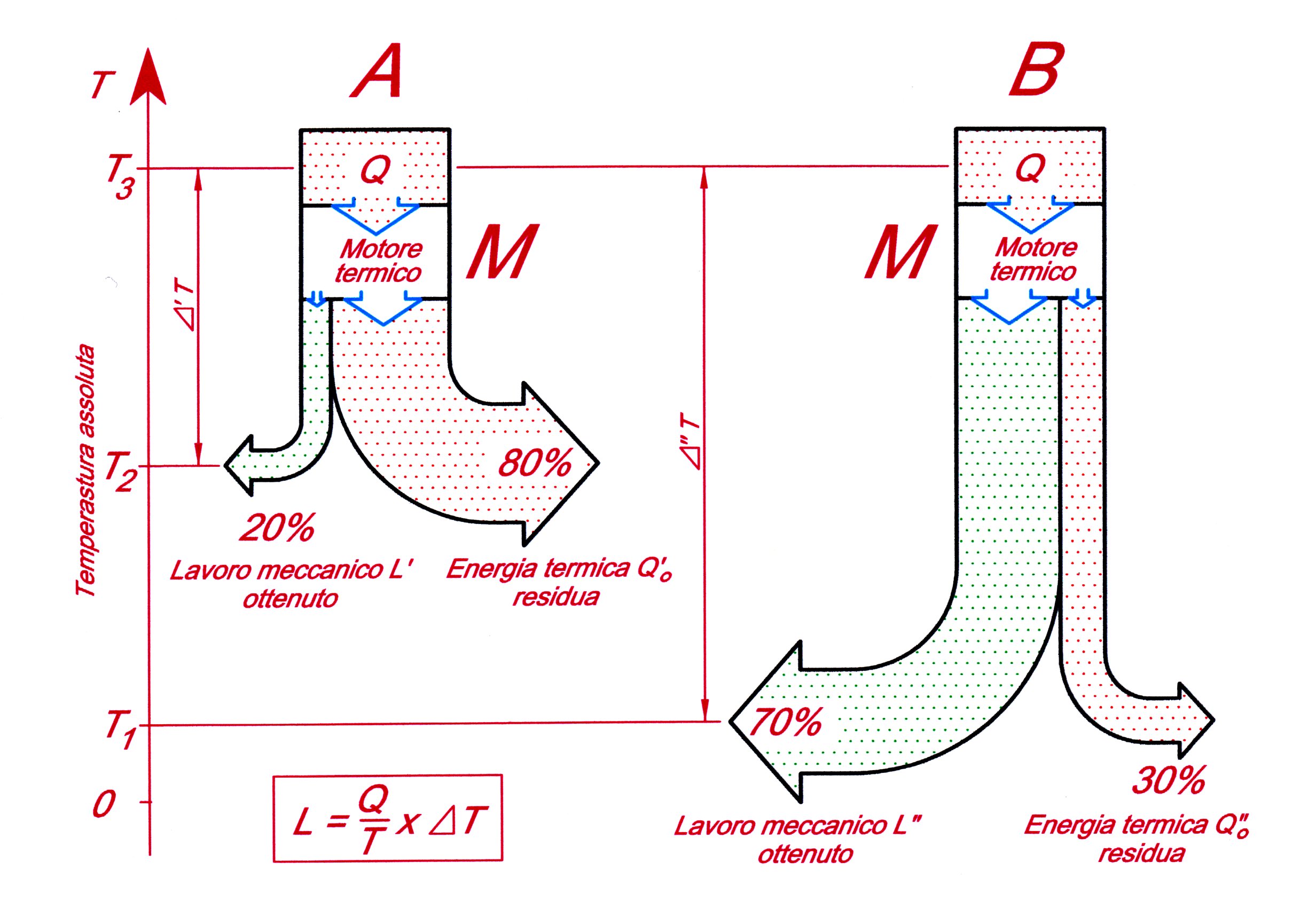
Figura 4 – Confronto tra il lavoro meccanico ottenuto da due motori termici identici funzionanti secondo il Ciclo Carnot per due diverse temperature di scarico


Ribadiamo che è necessario paragonare due casi ad Entropia iniziale identica (come in Figura 4) e tenere presente che è il fattore ΔT a determinare il risultato della trasformazione.
L’acqua del mare contiene enormi quantità di energia termica, ma ad una temperatura T praticamente identica a T_o: ciò rende inutilizzabile il calore in essa contenuto: possiamo affermare che l’acqua del mare possiede una ”grande” quantità di energia termica ma non esiste alcuna possibilità pratica di trasformarla in lavoro meccanico per mezzo di un motore termico (il salto entropico disponibile è “praticamente nullo”).


3. ENTROPIA E VITA

Livio Gratton (cosmologo triestino scomparso nel 1991 e considerato il padre dell’Astrofisica italiana) osservava che il fenomeno “vita” contiene qualcosa di singolare che non si inquadra nel meccanicismo fin qui descritto. La comparsa della vita, in un universo a struttura elettromagnetica, costituisce un momento singolare, che esula dalla logica meccanica, ed è scientificamente inspiegabile.
Infatti un organismo vivo è caratterizzato dal fatto che, al proprio interno, produce delle trasformazioni ad Entropia negativa (ovvero con ΔS<0) che contraddicono il secondo principio.
Osserviamo un seme vegetale: se è vivo, una volta create le condizioni previste dalla natura, germina spontaneamente e cresce catturando il Carbonio dall’atmosfera, dando corpo alla pianta, liberando l’Ossigeno.
Una pianticella di grano, appena nata, tra la neve, germina e cresce, riscaldandosi a spese dell’ambiente circostante (a chi non è capitato di osservare la neve fusa intorno alla pianticella, e le pianticelle quando, a manto di neve basso, fanno capolino e sono ben visibili, verdi germogli sulla trapunta bianca, con una macchiolina scura di terra, libera all’intorno?!).
Naturalmente se considerassimo anche l’interazione della pianta con i quanti solari e l’intorno minerale troveremmo che l’insieme delle trasformazioni ha generato dell’entropia positiva (giusta la nota affermazione che l’entropia dell’universo tende ad aumentare senza limiti).
Un organismo animale vivo, in caso di ferita, è in grado di ripararsi da sé: la vis vitalis, come la chiamavano i nostri antenati (ma qui non si pretende di darne una nuova definizione dopo i lavori di Wohler sull’Urea e la usiamo con diverso significato), produce tale effetto, mentre un organismo animale, morto, rimane ferito e marcisce col passare del tempo (incremento del disordine).
Si potrebbe riflettere sulla possibilità di ricorrere all’entropia per definire lo stato di vita o di morte su cui periodicamente ci si dibatte in casi pratici (Terry Schiavo, Eluana Englaro etc.): se l’organismo produce entropia negativa è vivo, in caso contrario no...
Si potrebbe, anche, suggerire una rozza procedura sperimentale, nel tentativo di risolvere la questione, consistente nel ferire un organismo di dubbia vitalità per verificarne le reazioni in un senso entropico o nell’altro...
La vis vitalis se ne va anche se tutti gli organi meccanici dovessero essere perfettamente funzionanti: pensiamo al cosiddetto arresto cardiaco (locuzione che appare un salvataggio in corner dell’arte medica). Certo si potrà obiettare che l’arresto è la causa e la dipartita della vis vitalis è l’effetto: mah!?, l’unica certezza è che con la morte inizia un processo irreversibile, verso il caos, con produzione di entropia positiva... e si rientra nei ranghi del secondo principio!
La proprietà più semplice e comune che si attribuisce all’Entropia è la seguente: in ogni trasformazione (irreversibile) l’Entropia finale è maggiore di quella iniziale, va, a questo punto, così arricchita: in ogni trasformazione (irreversibile) riguardante corpi inanimati l’Entropia etc. etc.
Come fare per produrre un riscaldamento della pianticella di grano a spese dell’universo circostante e ad incrementare l’ordine delle molecole fino a “costringere” il Carbonio, sottratto al più informe stato esistente (quello aeriforme), ad assumere la forma di un tronco dando luogo a delle trasformazioni ad entropia decrescente?


3. LA DISTRIBUZIONE DI BOLTZMANN

Risponderemo alla domanda dopo avere esaminato il secondo pilastro su cui basiamo questo saggio: la Distribuzione di Boltzmann (Ludwig Boltzmann, Austria 1844-1906).
Come si può vedere anche in eccellenti pagine sul web, le disordinate velocità di agitazione delle molecole di un gas (ma anche quelle dei liquidi e dei solidi), ad una data temperatura, assumono valori continuamente e casualmente variabili seguendo una distribuzione particolare, descritta in Figura 6 A, e rappresentata graficamente in Figura 5.



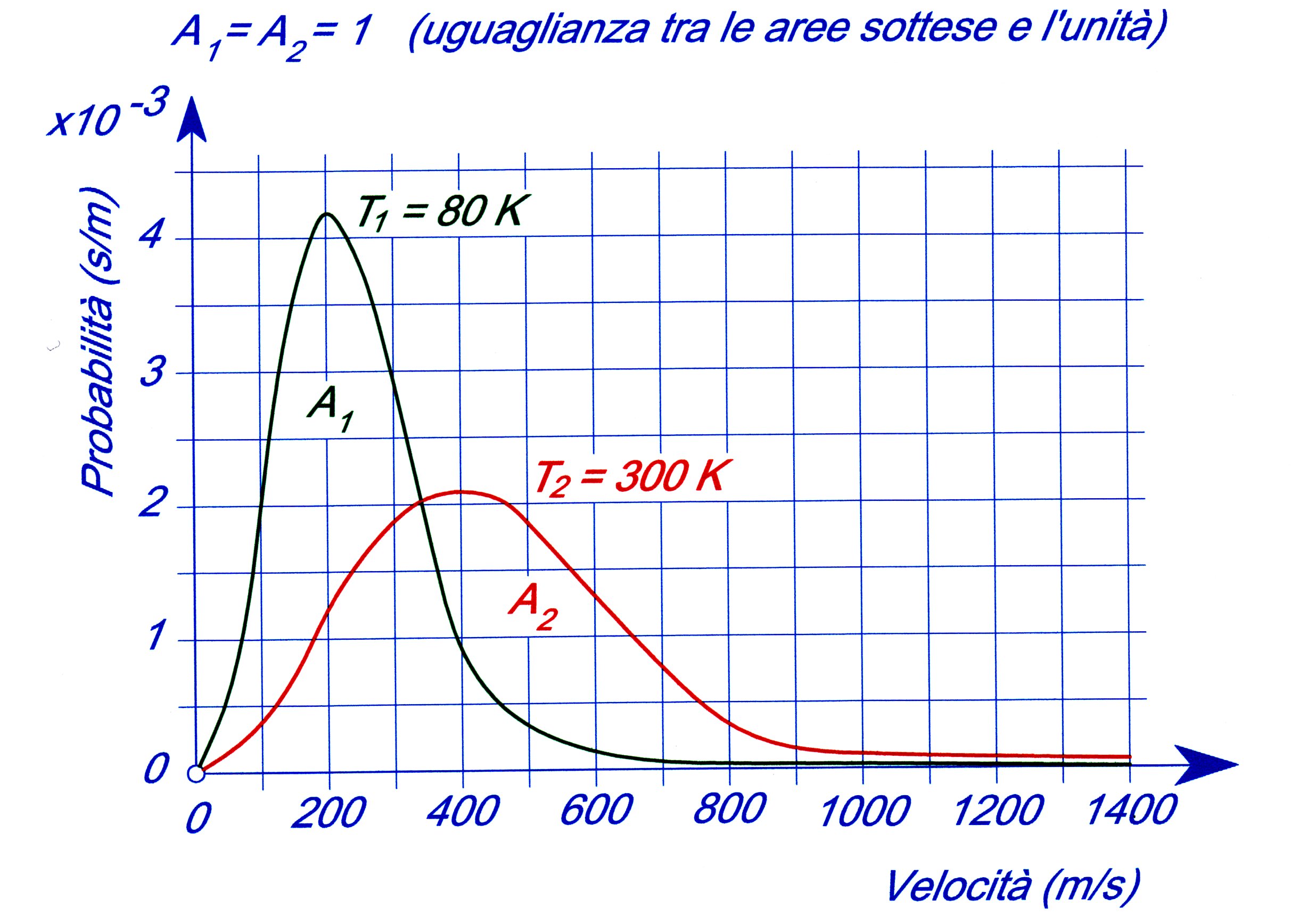
Figura 5 – Distribuzione della probabilità della velocità delle molecole di un gas in funzione della velocità stessa, secondo la Statistica di Boltzmann

E’ grazie a questa distribuzione, scoperta da Boltzmann, che la natura vivente, vegetale ed animale può effettuare trasformazioni locali ad entropia decrescente: i grandi Maestri hanno escogitato esperimenti pensati, basati su dispositivi in grado di selezionare le molecole del gas più freddo aventi velocità superiore alla velocità media ponderata delle molecole del gas più caldo (Maxwell: il folletto, Polvani: il portinaio cernitore, Amerio: la valvola selettrice) per lasciarle passare da un ambiente a temperatura minore ad un altro, contiguo, a temperatura maggiore ottenendo in questo modo una trasformazione che invalida localmente il secondo principio della termodinamica.
In Figura 6 A si vede che ad ogni velocità media (ponderata) delle molecole “calde” si può far corrispondere un ramo della curva “fredda” riguardante quelle particelle che, se passate dalla parte più calda, provocherebbero un incremento della stessa velocità media e, quindi, della temperatura.
E’ necessario fare una cernita delle molecole, una ad una, con mezzi meccanici di cui l’uomo non dispone mentre le osservazioni sperimentali, del tipo surriportato e riguardanti la vis vitalis, suggeriscono che la natura sia in grado di farlo, operando a livello molecolare nel campo degli organismi viventi.
In Figura 6B è rappresentato il dispositivo che consente l’”esperimento pensato” nella forma proposta dal prof. Amerio del Politecnico di Milano (1955). Maxwell aveva proposto un “folletto” come selettore delle molecole (1867): il dispositivo di selezione è stato oggetto di particolari attenzioni da parte di Szilard (1929) e, successivamente di Bennet (1981) con lo scopo di conteggiare correttamente la variazione di Entropia nell’universo di prova.


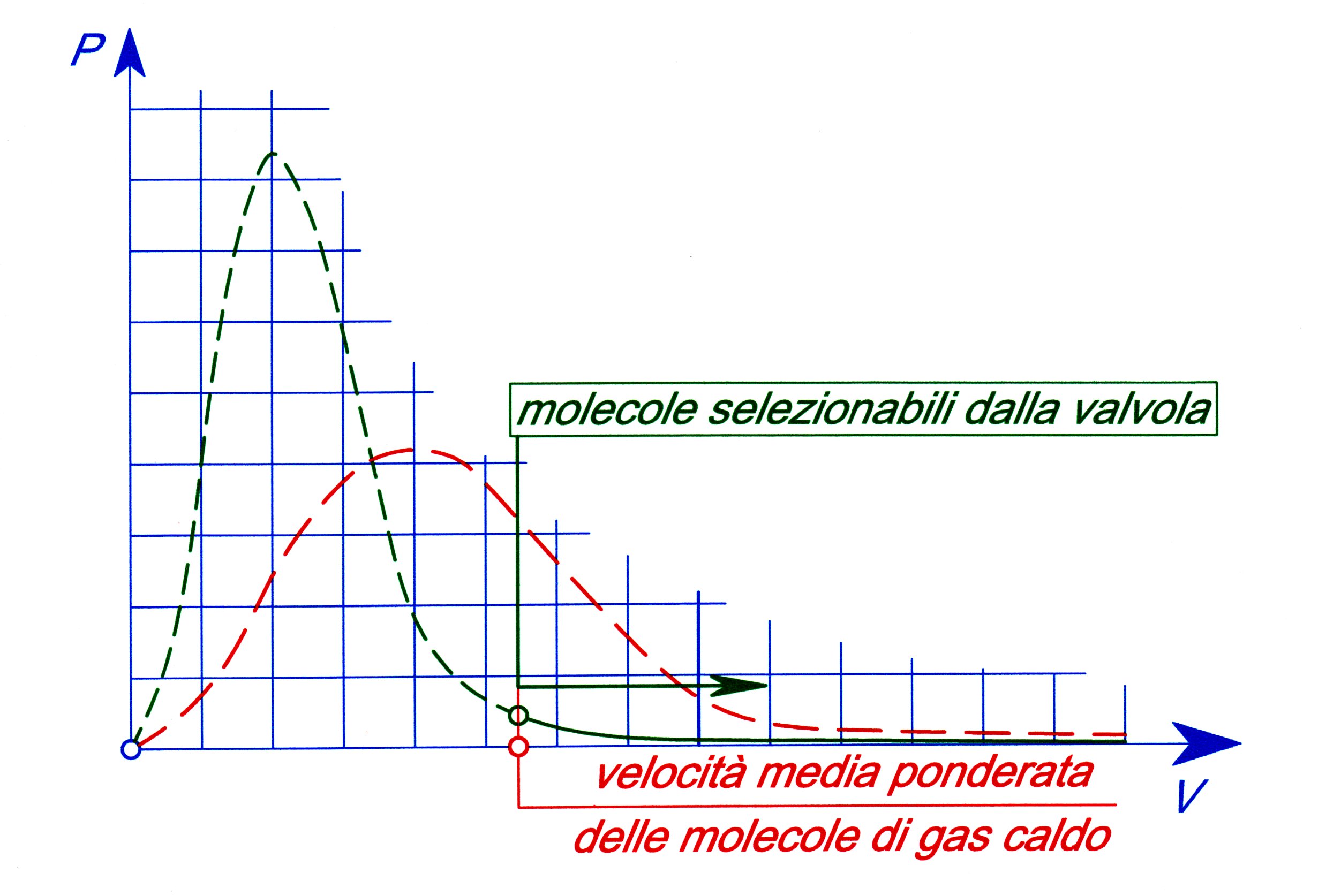
Figura 6 A

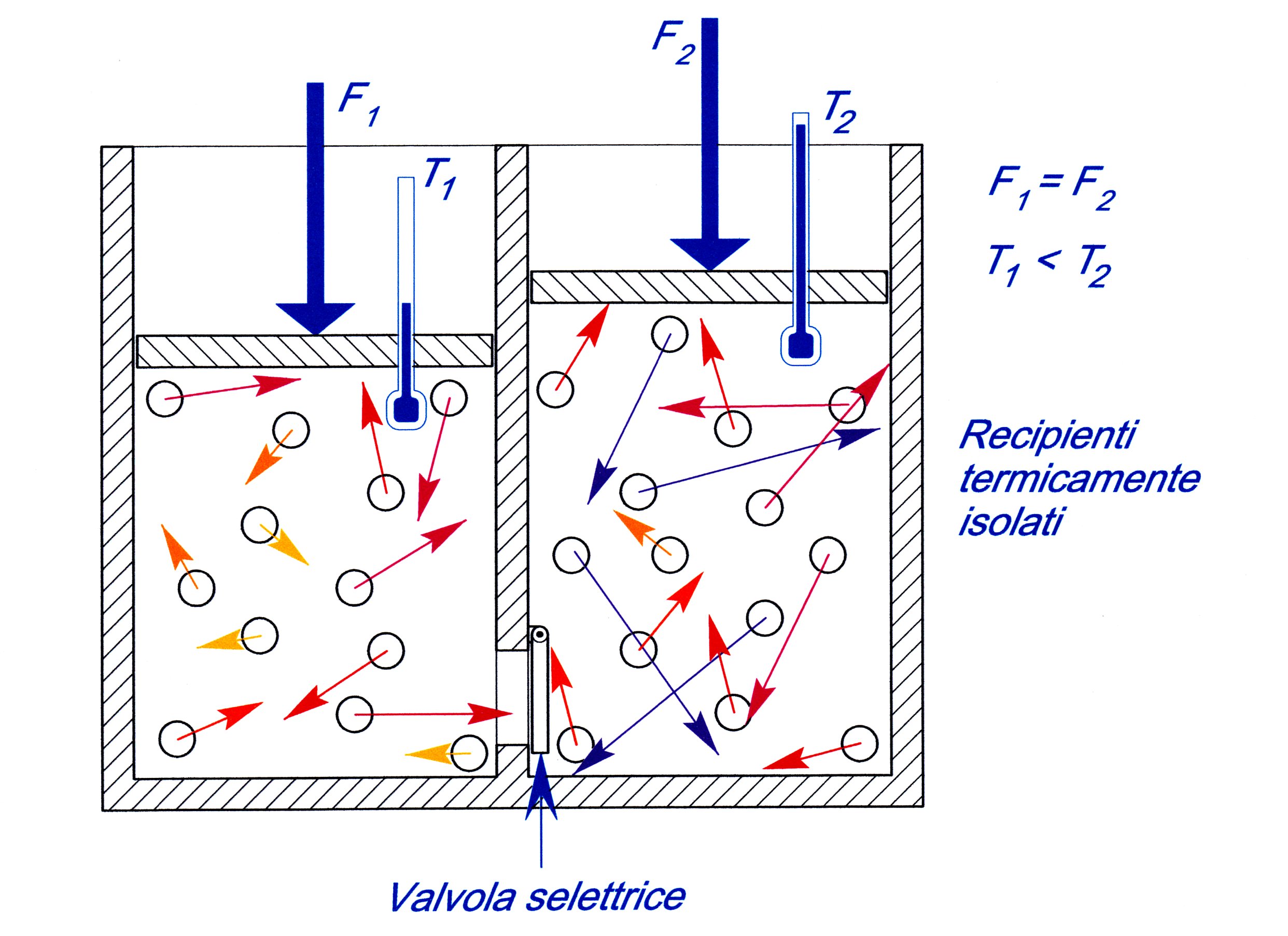
Figura 6 B


Figura 6 A e B – La valvola selettrice in B consente il passaggio dall’ambiente più freddo all’ambiente più caldo solo delle molecole che posseggono una velocità superiore alla velocità media ponderata delle particelle più calde, velocità che è posseduta da una piccola parte delle molecole “fredde”, come mostrato in A


Queste nostre elementari applicazioni di Termodinamica, dunque, basate sul concetto di Entropia e sulla Distribuzione di Boltzmann, ci suggeriscono che il fenomeno “vita” sia da associare ad una vis vitalis esterna alla meccanica dissipativa della quale abbiamo ampia e quotidiana esperienza.
Qualcuno tenta approcci sull’argomento con metodi impropri e con interpretazioni arbitrarie del concetto di probabilità boltzmaniana che portano a teorie prive del necessario rispetto di una sana dottrina scientifica.


4 CONCLUSIONE DELLA PRIMA PARTE

Sull’origine della vita sono stati scritti fiumi d’inchiostro sicché si possono leggere, in proposito, le teorie più stravaganti che ignorano completamente quanto suggerisce la Regina della Fisica: la Termodinamica.
Si disturba la Paleontologia, la Biologia, gli extraterrestri, gli UFO, la Palingenesi Cosmica et similia: non si usano numeri, equazioni, concetti di probabilità in termini corretti, principi di conservazione et similia che sono le uniche fondamenta per un discorso scientifico propriamente detto (non vi è aggettivazione più abusata del termine “scientifico”).
Il lettore potrà (magari in una domenica di pioggia, tanto per passare il tempo) fare qualche ricerca sul “brodo primordiale” (ma se non è Knorr, per la cui Casa, modestamente, in gioventù, abbiamo fatto progetti termotecnici, non è buono!...), sul “serbatoio cosmico”, sulle “scimmie dattilografe”, sul ciclo del Carbonio e dell’Ossigeno (a proposito della demonizzazione della CO₂), sul ciclo dell’acqua: argomenti trattati sostituendo la Scienza con l’ideologia e facendo ampio uso del principio d’autorità (l’ipse dixit di storica memoria) sostenendo dogmi sgangherati ma politicamente corretti.
Si noti che, nelle osservazioni fin qui fatte, non abbiamo parlato di energia il cui ruolo, nell’economia del nostro discorso, è secondario. E’ la “scoperta” dell’indice di stato Entropia che cambia il modo di vedere il cosmo: di essa non se ne parlerebbe se le trasformazioni realmente fattibili fossero reversibili.
Si potrebbe pensare che l’irreversibilità sia un "difetto" del cosmo avente la funzione di costringerlo ad un progressivo decadimento energetico in modo che la forma finale di tutta l’energia disponibile sia quella termica, ma entropicamente inutilizzabile: pertanto, in virtù di quanto discusso, ad un certo punto dell’evoluzione dell’universo, in un tempo finito, non sarà più possibile realizzare alcun ciclo termodinamico.



FINE DELLA PRIMA PARTE

TERMODINAMICA & VITA
Thermodynamics & life

Parte 2 di 2


1.2 LA PROBABILITA’ NELLA STATISTICA DI BOLTZMANN

Boltzmann ottenne il grafico della probabilità in funzione della temperatura postulando che, dato un certo numero m di particelle indistinguibili tra loro (che chiameremo A, B, C, ..., M), ed esistendo un numero n di stati possibili (a, b, c, ..., n) in cui una o più particelle (anche tutte m) si possono trovare, la presenza delle particelle in ciascuno stato possa avvenire con diverse possibilità.
Se le particelle identiche sono libere di occupare i vari stati (come nel caso di un gas), esse possono scambiarsi continuamente lo stato tra loro (p. es. grazie ad urti reciproci, come in Figura 6.1B, parte prima) pur mantenendo “mediamente” una certa distribuzione: a seconda delle condizioni al contorno (p.es. la temperatura) una certa distribuzione delle configurazioni possibili sarà tipica di tali condizioni.
Continuando nell’esempio se per stato della particella intendiamo il possesso di una certa quantità di energia cinetica E associata a ciascuna molecola di un gas, in un certo intervallo di valori d’energia ∆E ci saranno delle molecole in quantità costante anche se tra di loro avvengono continui scambi d’energia e, quindi, nell’ambito del medesimo intervallo, alcune particelle entrano ed altre escono.
Se, per necessità di immaginazione, in quel che segue le particelle saranno pensate come delle “palline” e gli stati come dei livelli energetici, le palline rappresenteranno le particelle, mentre i livelli rappresenteranno un intervallo energetico (∆E).
Partiamo da un caso molto semplice costituito da tre particelle (m=3) in grado di essere ospitate da due livelli (n=2), come illustrato nella Figura 1.2.
Nella colonna di sinistra vediamo tutte le combinazioni possibili, nella parte centrale vediamo che certe configurazioni si ripetono in modo tale che, se le particelle diventano indistinguibili (colonna 3), sono da ritenersi tra loro uguali.
Esistono, dunque, tre possibilità affinché si verifichi sia la combinazione 2,3,4 che la combinazione 5,6,7 ed una sola per la combinazione 1 e 8.
Se “normalizziamo” la possibilità (esprimendola in termini unitari o percentuali) essa assume il ruolo di probabilità (rapporto tra i casi favorevoli ed i casi possibili), cosa che abbiamo fatto nell’ultima colonna esprimendola, come d’uso, in termini percentuali. 



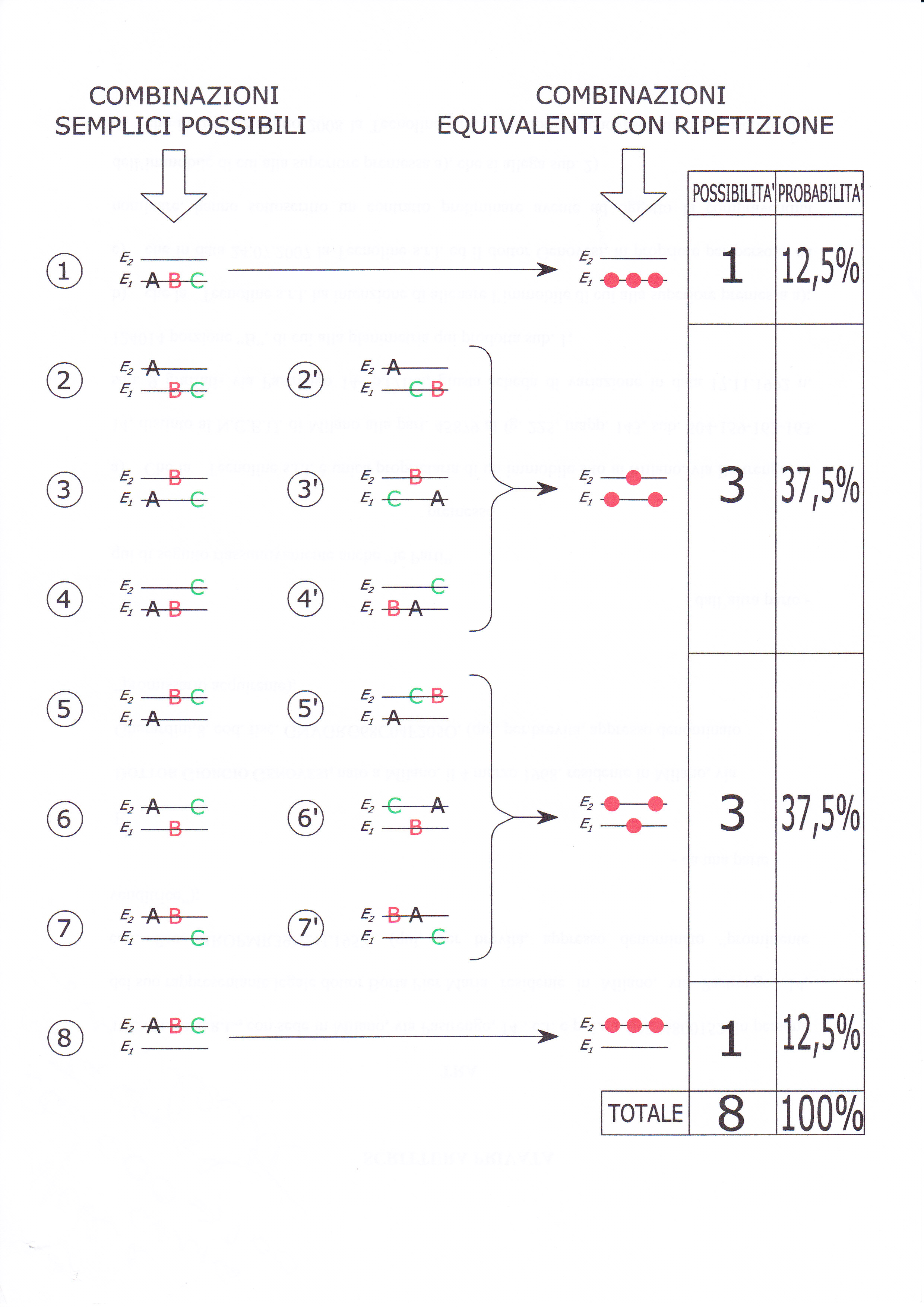
Figura 1.2 – Un caso assai semplice per mostrare come, dati m=3 ed n=2, si possano avere diverse probabilità per ciascuna combinazione 


Il tutto ci consente di disegnare il grafico di Figura 2.2 dove si comincia ad intravedere la formazione della boltzmaniana: 



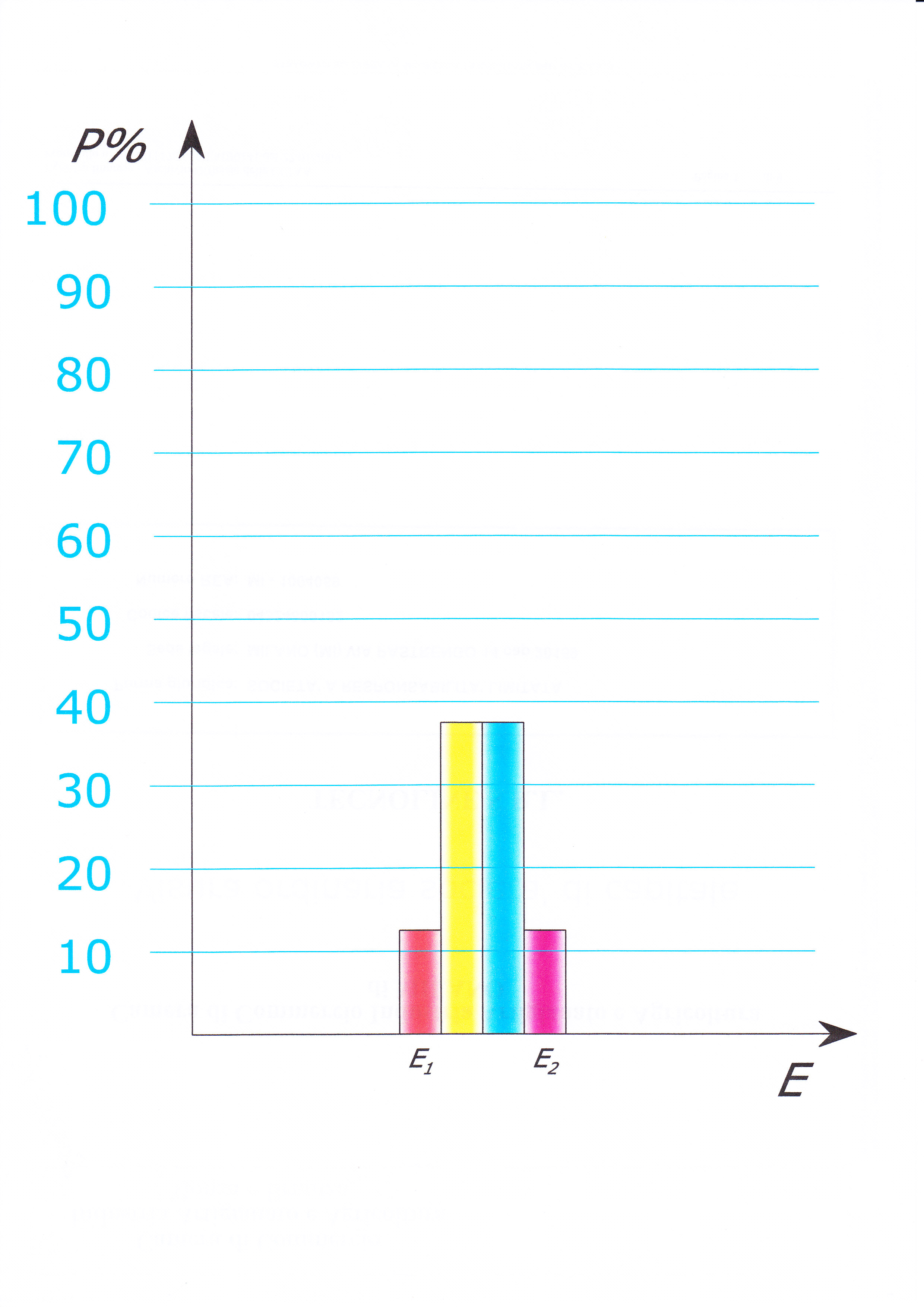
Figura 2.2 – La boltzmaniana in embrione: all’aumentare delle particelle e degli stati possibili l’inviluppo delle colonne acquisisce la caratteristica forma a campana asimmetrica


Sulle orme del grande Ludovico addentriamoci su sistemi numericamente più consistenti: nella Figura 3.2 sono rappresentate tre combinazioni e sette stati con arbitraria disposizione di quattro particelle; le tre combinazioni sono equivalenti perché le particelle sono indistinguibili per ipotesi. 

Figura 3.2 - Le tre configurazioni sono equivalenti se le quattro particelle sono indistinguibili tra loro 

Ciascuno degli n stati può essere associato sia ad A, che a B, che a C etc. (ovvero a ciascuna o più delle m particelle) e poiché una singola particella può occupare di volta in volta un certo stato (e le altre gli altri), per m volte, le combinazioni possibili C sono n×n×n×…×n (m fattori uguali a n) e, quindi,

C = n^m .

Ce ne possiamo convincere, anche, osservando, ad esempio, la Figura 4 dove si è assunto n=5 (sembra un pentagramma…) e si è considerato m=2 particelle (quindi 52=25 combinazioni):




piermariaboria@alice.it